DSA Bubble Sort Time Complexity

See the previous page for a general explanation of what time complexity is.

Bubble Sort Time Complexity

The Bubble Sort algorithm goes through an array of $n$ values $n-1$ times in a worst case scenario.

The first time the algorithm runs through the array, every value is compared to the next, and swaps the values if the left value is larger than the right. This means that the highest value bubbles up, and the unsorted part of the array becomes shorter and shorter until the sorting is done. So on average, $\frac{n}{2}$ elements are considered when the algorithm goes through the array comparing and swapping values.

We can start calculating the number of operations done by the Bubble Sort algorithm on $n$ values:

$$Operations = (n-1)\cdot \frac{n}{2} = \frac{n^2}{2} - \frac{n}{2}$$

When looking at the time complexity for algorithms, we look at very large data sets, meaning $n$ is a very big number. And for a very big number $n$, the term $\frac{n^2}{2}$ becomes a lot bigger than the term $\frac{n}{2}$. So large in fact, that we can approximate by simply removing that second term $\frac{n}{2}$.

$$Operations = \frac{n^2}{2} - \frac{n}{2} \approx \frac{n^2}{2} = \frac{1}{2} \cdot n^2$$

When we are looking at time complexity like we are here, using Big O notation, factors are disregarded, so factor $\frac{1}{2}$ is omitted. This means that the run time for the Bubble Sort algorithm can be described with time complexity, using Big O notation like this:

$$O( \frac{1}{2} \cdot n^2) = \underline{\underline{O(n^2)}}$$

And the graph describing the Bubble Sort time complexity looks like this:

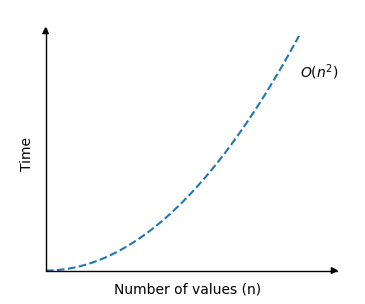
As you can see, the run time increases really fast when the size of the array is increased.

Luckily there are sorting algorithms that are faster than this, like Quicksort.

Bubble Sort Simulation

Choose the number of values in an array, and run this simulation to see how the number of operations Bubble Sort needs on an array of $n$ elements is $O(n^2)$:

The red line above represents the upper bound time complexity $O(n^2)$, and the actual function in this case is $1.05 \cdot n^2$.

A function $f(n)$ is said to be $O(g(n))$ if we have a positive constant $C$ so that $C \cdot g(n)>f(n)$ for a large number of values $n$.

In this case $f(n)$ is the number of operations used by Buble Sort, $g(n)=n^2$ and $C=1.05$.

Read more about Big O notation and time complexity on this page.